NHKラジオ朝一番のビジネス展望で「72の法則」なるものを知った。これは年
利率が与えられた時,複利計算で資産が元の2倍になるのに何年か
かるかが次の式で分かるというもの。
年利率(%) X 2倍になる年数=72
例えば年利率が7%のとき複利で増やすと約10年で2倍になるのです。 どうしてこうなるかを調べるべく「72の法則」でGoogle検索するとAll Aboutの"お金を2倍に増やす人が使う「72の法則」"がトップに表示されますが、なぜその式が成り立つのか書いていないので私の欲求を満たしてくれません。
そこでこの問題を私なりに考えて見る事にしました。
Aを元金、nを年数、rを年利率とするとn年後には
A(1+r)^n (^はべき数)
n年後に2倍になるのですから、元利合計は2A、従って次の式が成り立ちます。
A(1+r)^n=2A ここで両辺をAで割ると
(1+r)^n=2
計算をし易くする為、上式の自然対数を取ると
n*log(1+r)=log2 (logはeを底とする自然対数)
log2=0.693(関数電卓では2を押してからlnを押すと求まる)
n*log(1+r)=0.693 ・・・(1)
大分簡素な式になったが、log(1+r)の処理をどうしよう。ここでまたインターネット検索。どうもこの式はテイラー展開を使うといいらしい。
テイラー展開?何十年も前、大学の数学でやったが流石に式までは出て来なかった。そこでまたまたインターネットの世話に。
log(1+r)=r - r^2/2 + r^3/3・・・・・・ とあった。
概算に使うので第2項まで採用、すると
log(1+r)=r - r^2/2 これを(1)式に代入すると
n*(r-r^2/2)=0.693 nr=0.693+nr^2/2
この式でのrをパーセント表示にすると100を掛ける事になるので0.693は69.3、72に大分近づいて来た。問題はnr^2/2の処理。
このnrの正確な値はExcelで計算して見るとわかるので、やって見ることにした。
ここで使う関数はFV(Future Value)
現在価値:-1は1円を出金 数式の結果:2.011357188は約2円が入金
●15%の時は2倍になるのに5年
nr^2/2=5X0.15X0.15 / 2=0.056
●9.1%の時は2倍になるのに8年
nr^2/2=8X0.091X0.091 / 2=0.033
●7%の時は2倍になるのに10年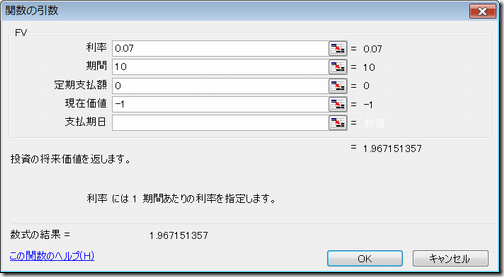
nr^2/2=10X0.07X0.07 / 2=0.025
●5%の時は2倍になるのに15年 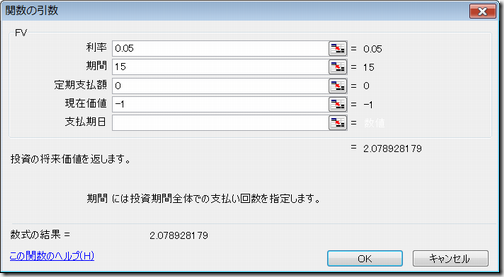
nr^2/2=15X0.05X0.05 / 2=0.019
●3%の時は2倍になるのに24年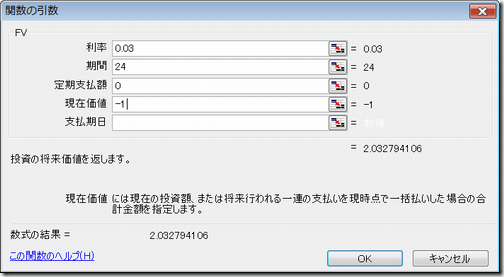
nr^2/2=24X0.03X0.03 / 2=0.011
この例で使ったnr^2/2の平均値は0.029
nr=0.693+0.029=0.722 rを%表示にするため両辺に100を掛けると
n(期間)X r(%)=72
こんな風に出して見ましたが、どうなんでしょうか。






